
George and Peter, dear friends for more than 50 years although totally different, are having their morning coffee arguing about life as they have done so many times in the past. George, the more pessimist and introvert between the two, takes a sip and says that he keeps his money in the bank as this way he feels safe, considering the unstable financial environment of modern times. It is important, he underlines, someone to secure their future. Peter, optimist and extrovert on the other hand, explodes and says that that money should always be available. Nothing bad will happen. What if he wants to go on an exotic trip with a new love that he might unexpectedly find?
Both friends know very well and agree that their lifetime savings is what is at stake in their argument. They disagree, however, on how possible it is that the flow of life events might dramatically change. The pessimistic view is afraid of the worst and the optimistic one is anticipating for the best.
The behavior of each one of the two friends reflects their confidence that life events are distinguished by their unique subjective assignment of probability of occurrence (Machina & Schmeidler 1992). In other words, George and Peter, in the absence of objective data to calculate how possible or impossible an event is to take place, they separately deal with (un)certainty with their own subjective perception mechanisms.
The rational decision making model of Expected Value, assumes that in order to choose an option, people multiply the perceived value of an outcome with the objective probability that this will take place. Behavioral Economics and Prospect Theory, slightly alter the aforementioned practice, assuming that people multiply the perceived value of an outcome with a special decision weight, based on personal subjective criteria (Kahneman & Tversky 1979).
George keeps his savings in closed bank accounts in order to take advantage of the higher interest rate and he does not normally open up to people he does not know. He pays much attention to certainty and avoids options that could generate unknown results. The special decision weight for George to choose an option is increasing as the probabilities of the option to happen are increasing. On the other hand, Peter ignores potential dangers always carrying a heavy wallet and he seeks for chances to meet new people. He pays much attention to life opportunities and likes to be exposed to the unknown. The special decision weight for Peter to choose an option is decreasing as the probabilities of the option to happen are increasing. However, relevant research underlines that, very often, probabilities’ weighting is neither solely “pessimistic” nor solely “optimistic” but a mix of the two instead (Fennema & Wakker, 1997).
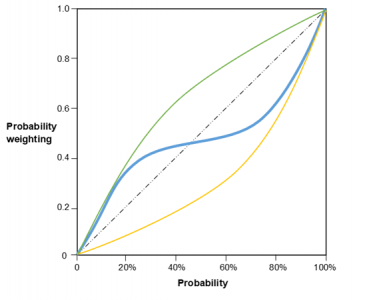
Let’s think the following dilemma: 2 lotteries offer the possibility to win 250€ each, the first with 5% probability and the second with 30% probability. You have the option to improve the chances of winning either A) from 5% to 10% in the first lottery or B) from 30% to 35% in the second. What would you choose? If your option was A then you agree with the 75% of the respondents of the research experiment of Gonzalez and Wu. Let’s now change the dilemma a bit: 2 lotteries again offer the possibility to win 250€ each, but the first with 65% probability and the second with 90% probability. You, now, have the option to improve the chances of winning either C) from 65% to 70% in the first lottery or D) from 90% to 95% in the second. What would you choose? If your option was D then you agree with the 72% of the respondents of the research experiment of Gonzalez and Wu. In other words, a 5% variation of the probability one outcome to take place is not always equally attractive (Gonzalez & Wu, 1999) and may get different weighting each time!
The aforementioned example confirms the notion of probability weighting function which, based on relevant research, is concave for low probabilities gradually changing into convex for high probabilities (Diecidue & Wakker, 2000). Imagine instead a function line that looks like an inverse-S. Such weighting (or sensitivity) change suggests low sensitivity in probability changes away from the absolutely impossible 0% and the absolutely certain 100% (Kahneman, 2013).
With or without ups-and-downs in regards to how sensitive we are to the uncertain, the analysis of probabilities is a notorious subject for centuries now, as it was described in the previous article. “The chance of gain is naturally overvalued, we may learn from the universal success of lotteries. The world neither ever saw, nor ever will see, a perfectly fair lottery; or one in which the whole gain compensated the whole loss; because the undertaker could make nothing by it” (Adam Smith, 1776).
Can you, perhaps, think of a reason that makes us indifferent to changes of the probabilities of an outcome to take place? Is everyone interested to lotteries? Which curve lines describe the stereotypical profiles of the two friends in the introductory example?
References
- Diecidue, E. and Wakker, P. (2000). On The Intuition of Rank-Dependent Utility. SSRN Electronic Journal.
- Fennema and Wakker (1997), “Original and Cumulative Prospect Theory: A Discussion of Empirical Differences,” Journal of Behavioral Decision Making, 10, 53-64.
- Kahneman, D. (2013). Thinking, fast and slow. New York: Farrar, Straus and Giroux.
- Kahneman and Tversky (1979), “Prospect Theory: An Analysis of Decision under Risk”, Econometrica, 47, 263-292.
- Machina, M. J., and Schmeidler D. (1992): “A More Robust Definition of Subjective Probability,” Econometrica, 60, 745–780
- Smith (1776). An Inquiry into the Nature and Causes of the Wealth of Nations [ed. by Roy H. Campbell and Andrew. S. Skinner], Oxford: Clarendon Press, 1976.
