Shall I take the risk? Or leave it up to fortune? There might not be one absolute answer since every decision is different. Even the same person can make different choices in different times for the same dilemma (Thaler and Shefrin, 1981).
Let’s then try to describe the meaning of concepts such as risk, uncertainty and luck, words that we use very often in our everyday life and make an attempt to better approach the expected, the unexpected or the unknown. Is it possible to foresee them?
Although the divine substance was solely responsible for the explanation of the fate of mankind, the concept of risk was born in Europe during the 13th century from merchants and seafarers while they were trying to calculate potential future damages connected to their profession (Luhmann, 1993). Later on in the 16th century, the great mathematicians of the time started making attempts to conventionalize risk with formulas. And long enough later, statistics and economics simply described that risk refers to future events for which we know the probabilities of emergence (Keen, 2011). For example, 50% a toss of a coin to result heads or tails, 48,6% a roulette to point to red or black. Uncertainty, on the other hand, has to do with future events for which we don’t know the probabilities of emergence (Keynes, 1921) and got independent as a concept in the beginning of the 20th century. We know, in other words that we may get a salary raise or that tomorrow it might rain, however we cannot say for sure how possible those are. Lastly, when it comes to luck, the oldest of the three concepts, everything is open. We are neither in a position to know what event may take place nor with which probability of course (Dudley, 2012).
The idea of chasing an unpredictable fate, might captivate some people, however, it is logical others to try to deal with casual and uncertain situations as if they were just risky. Is it possible, though, to calculate the probabilities each time or do we fall in the fallacy of Fortuna?
Behavioral Economics remind us that in the analysis of probabilities as well, we make logical mistakes which we don’t understand at first sight. In one of their experiments in the 1980s, Kahneman and Tversky introduced Linda to young university students. Linda is a 31-year-old woman, bright, extrovert and single. She has studied philosophy and during her student years she participated in anti-nuclear demonstrations as she was deeply concerned with issues of social justice (Tversky and Kahneman, 1983). Then, the students were asked to answer which of the following scenarios seems more possible:
1) Linda is a bank executive or
2) Linda is a bank executive and an active in the feminist movement
More than 85% answered that the 2nd scenario is more possible. This answer, however, is not in line with the basic principles of statistics concerning probabilities. Probability is an arithmetic forecast based on relevant past events/experiments. More precisely, probability is the degree to which an event may occur and is measured as a fraction with nominator the cases where the event occurs and denominator all the cases where it could occur (Laplace, 1812).

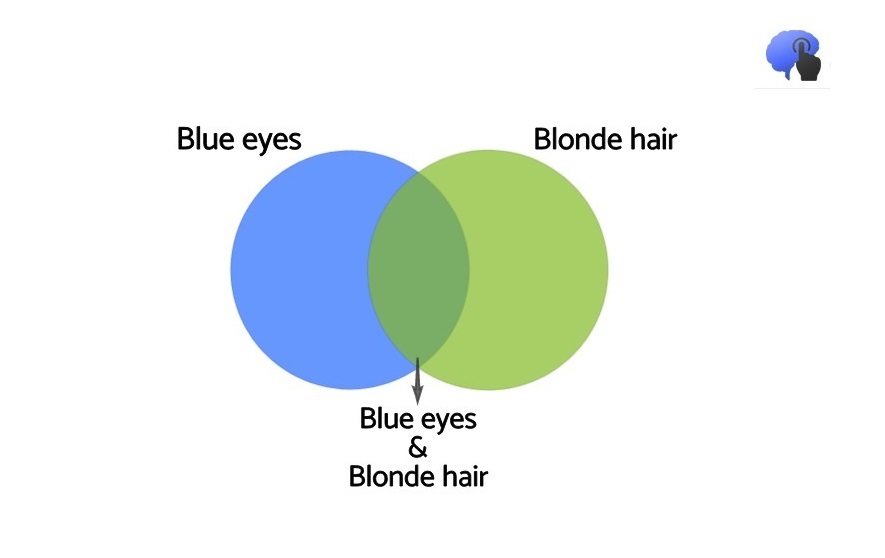
Back to the imaginary character of Linda, both of the proposed scenarios have their individual probabilities, which we may not be able to calculate. Nevertheless, for one thing we can be sure: the case where both the scenarios are taking place, in other words the combined event, should be less probable. Linda, the feminist bank executive, managed then to give birth to the concept of “Conjunction Fallacy” according to which people tend to evaluate the conjunction of two events to be more probable than just one of them (Kahneman, 2013). In other words, how is it possible the probability where Bjorn has blonde hair and blue eyes to be greater than the probability he just has blonde hair?
Some might, logically, say that sports betting is maybe one of the grater field of probabilities’ analysis. However, even the most experienced players fall in the trap of the Conjunction Fallacy in the cases of combined events and probabilities (Erceg and Galić, 2014). If, for example, we assume that the probability Milan to beat Fiorentina is 40% and Liverpool to beat Wigan is 60%, how is it possible the probability of the simultaneous wins of Milan and Liverpool to be greater than 24%? (Nilsson and Andersson, 2010). Imagine what terrifying margins for profit could this fallacy of calculating probabilities generate?
As most of behavioral theories, the Conjunction Fallacy has received critique, among the academic community, mainly in regards to the way probable events are described. It has been noticed that if the different scenarios are demonstrated as percentages, for instance “How many bank executives would exist among 100 Lindas?”, the mistaken answers decrease but not dramatically (Gigerenzer, 1991). Some might say, then, that Fortuna manages to befool us even when we pay attention? Or do we pay enough of it?
References
- Gigerenzer, G. (1991). How to Make Cognitive Illusions Disappear: Beyond “Heuristics and Biases”. European Review of Social Psychology, 2(1), pp.83-115.
- Dudley, J. (2012). Aristotle’s Concept of Chance.
- Erceg, N. and Galić, Z. (2014). Overconfidence bias and conjunction fallacy in predicting outcomes of football matches. Journal of Economic Psychology, 42, pp.52-62.
- Kahneman, D. (2013). Thinking, fast and slow. New York: Farrar, Straus and Giroux.
- Keen, S. (2011). Debunking economics – revised and expanded edition. London: Zed, p.226.
- Keynes, J. (1921). A treatise on probability. London: Macmillan.
- Laplace, M. (2012). Philosophical Essay on Probabilities (1812). Dover Publications.
- Luhmann, N. (1993). Risk: a sociological theory. Berlin: de Gruyter.
- Nilsson, H. and Andersson, P. (2010). Making the seemingly impossible appear possible: Effects of conjunction fallacies in evaluations of bets on football games. Journal of Economic Psychology, 31(2), pp.172-180.
- Thaler, Richard H., and H. Shefrin (1981), “An Economic Theory of Self-Control,” Journal of
- Political Economy, 89, 392-406.
- Tversky, A., and Kahneman, D. (1983). “Extensional Versus Intuitive reasoning: The Conjunction Fallacy in Probability Judgment,” Psychol. Rev. 90, 4.
