Να πάρω το ρίσκο ή να το αφήσω στην τύχη του; Απόλυτη απάντηση δεν υπάρχει μιας και τα δεδομένα κάθε απόφασης διαφέρουν. Και όπως επιβεβαιώνει καθημερινά η ανθρώπινη συμπεριφορά, ακόμα και το ίδιο άτομο μπορεί για ένα ζήτημα να κάνει διαφορετικές επιλογές σε διαφορετικά χρονικά σημεία (Thaler and Shefrin, 1981).
Θα επιχειρήσουμε, λοιπόν, να περιγράψουμε τη σημασία εννοιών όπως το ρίσκο, η αβεβαιότητα και η τύχη, λέξεις που χρησιμοποιούμε συνεχώς στην καθημερινότητά μας, σε μια προσπάθεια να κατανοήσουμε καλύτερα το αναμενόμενο, το αναπάντεχο, το άγνωστο. Μπορούμε, άραγε, να το προβλέψουμε;
Παρότι η θεϊκή υπόσταση ήταν αποκλειστικά υπεύθυνη για την εξήγηση της ανθρώπινης μοίρας, το ρίσκο σαν έννοια γεννήθηκε στην Ευρώπη του 13ου αιώνα από εμπόρους και θαλασσοπόρους στην προσπάθειά τους να υπολογίσουν τους πρακτικούς κινδύνους του επαγγέλματος (Luhmann, 1993). Αρκετά αργότερα, τον 16ο αιώνα πλέον, είναι που οι μαθηματικοί της εποχής επιδιώκουν να το τυποποιήσουν με συναρτήσεις. Και αρκετά χρόνια μετά η στατιστική με την οικονομία εξηγούν απλά πως το ρίσκο αναφέρεται σε μελλοντικά ενδεχόμενα των οποίων γνωρίζουμε τις πιθανότητες εμφάνισής τους (Keen, 2011). Για παράδειγμα, 50% να έρθει ένα νόμισμα κορώνα έναντι 50% γράμματα, 48.6% μια ρουλέτα να φέρει μαύρο ή κόκκινο. Η αβεβαιότητα, από την άλλη, περιγράφει μια κατάσταση από ενδεχόμενα για τα οποία δεν γνωρίζουμε την κατανομή των πιθανοτήτων (Keynes, 1921) και αυτονομήθηκε σαν έννοια στις αρχές του 20ου αιώνα. Ξέρουμε, δηλαδή, ότι μπορεί να πάρουμε αύξηση ή ότι ίσως αύριο βρέξει, όμως δε μπορούμε να πούμε με απόλυτη σιγουριά πόσο πιθανά είναι αυτά. Τέλος, στο θέμα τύχη, την αρχαιότερη από τις τρεις λέξεις, τα πάντα είναι ανοιχτά. Δεν γνωρίζουμε ούτε τι μπορεί να συμβεί ούτε, φυσικά, με τι πιθανότητα (Dudley, 2012).
Το «μοιραίο» ίσως ορισμένους να τους σαγηνεύει, ωστόσο είναι, θα ΄έλεγε κανείς, επόμενο οι άνθρωποι να θέλουμε να αντιμετωπίσουμε πολλές τυχαίες ή αβέβαιες καταστάσεις ως ρίσκο. Είναι δυνατόν, όμως, να αξιολογήσουμε τις πιθανότητες ή πέφτουμε αναπόφευκτα στην πλάνη της Θεάς Τύχης;
Τα συμπεριφορικά οικονομικά μας υπενθυμίζουν, πως και στην ανάλυση πιθανοτήτων κάνουμε λάθη τα οποία δεν αντιλαμβανόμαστε. Οι Kahneman και Tversky, σε ένα από πειράματά τους στις αρχές του ‘80, παρουσίασαν σε νεαρούς σπουδαστές την Λίντα. Η Λίντα είναι μια κοπέλα 31 ετών, έξυπνη, εξωστρεφής και δεν έχει παντρευτεί. Έχει σπουδάσει φιλοσοφία και στα νιάτα της συμμετείχε σε διαδηλώσεις κατά των πυρηνικών μιας και είχε ιδιαίτερη ευαισθησία σε ζητήματα κοινωνικής δικαιοσύνης (Tversky and Kahneman, 1983). Έπειτα, ζητήθηκε από τους φοιτητές να απαντήσουν πιο από τα παρακάτω ενδεχόμενα τους φαίνεται πιο πιθανό:
- Η Λίντα να εργάζεται ως τραπεζικό στέλεχος ή
- Η Λίντα να εργάζεται ως τραπεζικό στέλεχος και να είναι ενεργό μέλος του φεμινιστικού κινήματος
Περισσότεροι από το 85% απάντησαν πως το 2ο ενδεχόμενο είναι πιο πιθανό. Η απάντηση, όμως, αυτή, δε συνάδει με τα όσα μας μαθαίνει η στατιστική για τις πιθανότητες. Η πιθανότητα είναι μια αριθμητική πρόβλεψη βασισμένη σε συγγενή παρελθόντα δεδομένα/πειράματα. Πιο συγκεκριμένα ο βαθμός κατά τον οποίο ένα ενδεχόμενο μπορεί να συμβεί και μετράται σαν το κλάσμα των περιπτώσεων που το ενδεχόμενο εμφανίζεται ως προς το σύνολο των περιπτώσεων που θα ήταν δυνατόν να εμφανιστεί (Laplace, 1812).

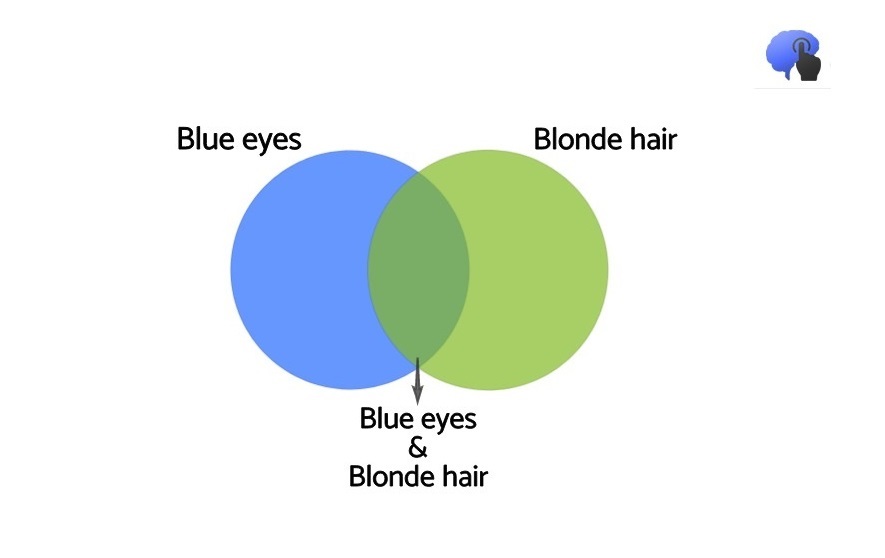
Για την φανταστική φυσιογνωμία της Λίντα, το καθένα από τα δύο ενδεχόμενα έχει μια πιθανότητα εμφάνισης που ίσως να μην μπορούμε να υπολογίσουμε με ακρίβεια. Ωστόσο αυτό που μπορούμε να πούμε με σιγουριά είναι πως η περίπτωση να ισχύουν και τα δυο ταυτόχρονα, με άλλα λόγια το συνδυαστικό ενδεχόμενο, πρέπει να συγκεντρώνει λιγότερες πιθανότητες. Η φεμινίστρια τραπεζίτης Λίντα, λοιπόν, γέννησε την έννοια της «Πλάνης της Σύζευξης» (Conjunction Fallacy) κατά την οποία οι άνθρωποι τείνουν να αξιολογούν την πιθανότητα δύο ενδεχόμενα να συμβούν ταυτόχρονα ως μεγαλύτερη από την πιθανότητα να συμβεί μόνο το ένα (Kahneman, 2013). Με άλλα λόγια είναι δυνατόν η πιθανότητα ο Bjorn να έχει ξανθά μαλλιά και γαλάζια μάτια να είναι μεγαλύτερη από εκείνη να έχει απλά ξανθά μαλλιά;
Είναι επόμενο να σκεφτεί κανείς, πως ένα από τα μεγαλύτερα πεδία ανάλυσης πιθανοτήτων είναι οι δημοφιλείς αθλητικές στοιχηματικές συνήθειες. Ακόμα και εκεί, όμως, οι πεπειραμένοι στοιχηματικοί παίκτες πέφτουν θύματα της «Πλάνης της Σύζευξης» όταν οι πιθανότητες συνδυάζονται (Erceg and Galić, 2014). Εάν, για παράδειγμα, θεωρούμε πως η πιθανότητα η Milan να κερδίσει την Fiorentina είναι 40% και η Liverpool να κερδίσει την Wigan 60%, πώς είναι δυνατόν οι ταυτόχρονες νίκες των Milan και Liverpool να θεωρούμε πως θα συμβούν με πιθανότητα μεγαλύτερη από 24%; (Nilsson and Andersson, 2010). Φανταστείτε τι τρομακτικά περιθώρια για κέρδος μπορεί να δημιουργήσει η πλάνη του υπολογισμού συνδυασμένων πιθανοτήτων;
Όπως και οι περισσότερες θεωρίες συμπεριφοράς, η «Πλάνης της Σύζευξης» έχει κι αυτή δεχθεί κριτική κυρίως σχετικά με τον τρόπο περιγραφής των ενδεχομένων. Έχει παρατηρηθεί πως αν τα σενάρια παρουσιάζονται ως ποσοστιαίες πιθανότητες, για παράδειγμα «στις 100 Λίντα πόσες απο αυτές είναι τραπεζικοί;», οι λάθος απαντήσεις μειώνονται, χωρίς, όμως να απαλείφονται (Gigerenzer, 1991). Καταφέρνει, δηλαδή, η Θεά Τύχη να μας ξεγελάει ακόμα και όταν δίνουμε προσοχή; Ή μήπως δεν δίνουμε αρκετή;
Πηγές
- Gigerenzer, G. (1991). How to Make Cognitive Illusions Disappear: Beyond “Heuristics and Biases”. European Review of Social Psychology, 2(1), pp.83-115.
- Dudley, J. (2012). Aristotle’s Concept of Chance.
- Erceg, N. and Galić, Z. (2014). Overconfidence bias and conjunction fallacy in predicting outcomes of football matches. Journal of Economic Psychology, 42, pp.52-62.
- Kahneman, D. (2013). Thinking, fast and slow. New York: Farrar, Straus and Giroux.
- Keen, S. (2011). Debunking economics – revised and expanded edition. London: Zed, p.226.
- Keynes, J. (1921). A treatise on probability. London: Macmillan.
- Laplace, M. (2012). Philosophical Essay on Probabilities (1812). Dover Publications.
- Luhmann, N. (1993). Risk: a sociological theory. Berlin: de Gruyter.
- Nilsson, H. and Andersson, P. (2010). Making the seemingly impossible appear possible: Effects of conjunction fallacies in evaluations of bets on football games. Journal of Economic Psychology, 31(2), pp.172-180.
- Thaler, Richard H., and H. Shefrin (1981), “An Economic Theory of Self-Control,” Journal of
- Political Economy, 89, 392-406.
- Tversky, A., and Kahneman, D. (1983). “Extensional Versus Intuitive reasoning: The Conjunction Fallacy in Probability Judgment,” Psychol. Rev. 90, 4.
